Problem I
Circles in Triangle
Input: standard input
Output: standard output
Time Limit: 3 seconds

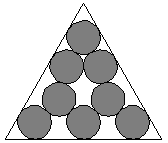
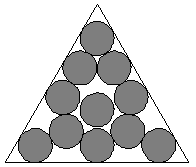
The pictures below show how one can put eight or eleven circles optimally in an equilateral triangle. In this problem you will have to find out the minimum possible side of an equilateral triangle which can hold 8 and 11 circles of certain radius. For the pictures below you can assume

1. Whenever a circle appears to touch a side of the triangle it actually touches it.

2. In the second figure the circle at the center does not touch any other circle.

Fig: Eight circles in an equilateral triangle.	Fig: Eleven circles in an equilateral triangle

Input

First line of the input file contains an integer N which indicates how many lines of inputs are to follow. Each of the next N lines contains a single floating point number r (r < 10000), which indicates the radius of the circles to be put inside the triangles. Input is terminated by end of file.

Output

For each line of input produce one line of output. This line should contain two floating-point numbers S₈ and S₁₁. Here S₈ is the minimum possible side of an equilateral triangle which can hold eight circles of radius r. S₁₁ has similar meaning. All the floating point numbers should have ten digits after the decimal point. The output will be checked with special correction programs. So small precision errors (less than max (1e-8, 1e-6%)) will be ignored.

Sample Input
3

0.000000001

0.000000002

0.000000003

Sample Output
0.0000000093 0.0000000107

0.0000000186 0.0000000215

0.0000000279 0.0000000322

---

(Regionals 2002 Warm-up Contest, Problem setter: Shahriar Manzoor)