Problem G

Matrix

Input: Standard Input

Output: Standard Output

Time Limit: 2 Seconds

 

[Preliminaries]

(He who has already studied linear algebra may skip this part)

A matrix is composed of n*n elements. Formally,

 is an n*n matrix.



for example,  is a 2*2 matrix.



Two operations on matrices will be used in this problem:


1. A + k (A is an n*n matrix, k is an integer)

all the elements in the MAIN diagonal is added by k. that is



 

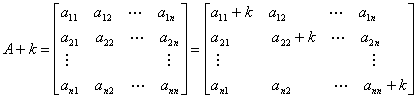
For example,

. A-k is defined A+(-k), so



 

2. A*B (both A and B are n*n matrices), let

, ,




and

,



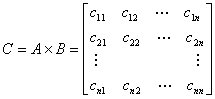then we have:



For example,



 

Well, I have no time to explain why matrix multiplication is defined like this. Please just remember it.

 

[Problem]

Find a matrix root of this equation:


(A + k1)(A+k2)(A+k3)...(A+km) = O where k1,k2...km are distinct integers.


That is, EVERY ELEMENT OF the matrix computed from the left is zero.

for example,

 is a matrix root of the equation(A+1)(A-5) = O，since



It can be proven that there are infinitely many solutions, however, I do not like trivial answer, so your answer must have at least (n*n)/2 non-zero elements.

 

Input

The first line contains the number of tests t(1<=t<=15). Each case contains two lines. The first line contains an integer m(1<=m<=30). The second line contains m integeres, representing k1,k2...km respectively. Absolute values of the integers are no greater than 100.

 

Output

For each test case, if no answer can be found, print -1. otherwise print n, indicating that you found an n*n matrix root. the following n lines should be the matrix. It is guaranteed that if there is an answer, the smallest possible n is not greater than 50, so your n should also NOT be greater than 50. The absolute value of integers you gave should not be larger than 1000.

 

Sample Input                             Output for Sample Input

2

2

1 -5

2

1 -5

2

1 4

2 3

2

1 4

2 3

Problemsetter: Rujia Liu, Member of Elite Problemsetters' Panel

Special thanks to Monirul Hasan