Problem A
Play with Floor and Ceil
Input: standard input
Output: standard output
Time Limit: 1 second

Theorem

For any two integers x and k there exists two more integers p and q such that:

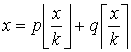
It’s a fairly easy task to prove this theorem, so we’d not ask you to do that. We’d ask for something even easier! Given the values of x and k, you’d only need to find integers p and q that satisfies the given equation.

Input

The first line of the input contains an integer, T (1≤T≤1000) that gives you the number of test cases. In each of the following T lines you’d be given two positive integers x and k. You can safely assume that x and k will always be less than 10⁸.

Output

For each of the test cases print two integers: p and q in one line. These two integers are to be separated by a single space. If there are multiple pairs of p and q that satisfy the equation, any one would do. But to help us keep our task simple, please make sure that the values, and fit in a 64 bit signed integer.

Sample Input Output for Sample Input

3 5 2 40 2 24444 6

1 1 1 1 0 6

---

Problem setter: Monirul Hasan, Member of Elite Problemsetters' Panel

Special Thanks: Shahriar Manzoor, Member of Elite Problemsetters' Panel