Problem X
Huge Mod
Input: standard input
Output: standard output
Time Limit: 1 second
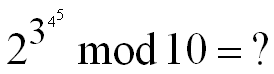 The operator for exponentiation is different from the addition, subtraction, multiplication or division operators in the sense that the default associativity for exponentiation goes right to left instead of left to right. So unless we mess it up by placing parenthesis,
The operator for exponentiation is different from the addition, subtraction, multiplication or division operators in the sense that the default associativity for exponentiation goes right to left instead of left to right. So unless we mess it up by placing parenthesis, 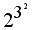 should mean
should mean 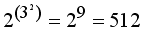 not
not 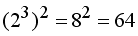 . This leads to the obvious fact that if we take the levels of exponents higher (i.e., 2^3^4^5^3), the numbers can become quite big. But let's not make life miserable. We being the good guys would force the ultimate value to be no more than 10000.
. This leads to the obvious fact that if we take the levels of exponents higher (i.e., 2^3^4^5^3), the numbers can become quite big. But let's not make life miserable. We being the good guys would force the ultimate value to be no more than 10000.
Given a1, a2, a3, ... , aN and m(=10000)
you only need to compute a1^a2^a3^...^aN mod m.
Input
There can be multiple (not more than 100) test cases. Each test case will be presented in a single line. The first line of each test case would contain the value for M(2<=M<=10000). The next number of that line would be N(1<=N<=10). Then N numbers - the values for a1, a2, a3, ... , aN would follow. You can safely assume that 1<=ai<=1000. The end of input is marked by a line containing a single hash ('#') mark.
Output
For each of the test cases, print the test case number followed by the value of a1^a2^a3^...^aN mod m on one line. The sample output shows the exact format for printing the test case number.
Sample Input | Sample Output |
10 4 2 3 4 5
100 2 5 2
53 3 2 3 2
#
|
Case #1: 2
Case #2: 25
Case #3: 35
|
Problem setter: Monirul Hasan, Member of Elite Problemsetters' Panel
Special thanks: Mohammad Sajjad Hossain
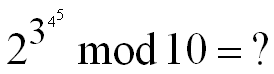 The operator for exponentiation is different from the addition, subtraction, multiplication or division operators in the sense that the default associativity for exponentiation goes right to left instead of left to right. So unless we mess it up by placing parenthesis,
The operator for exponentiation is different from the addition, subtraction, multiplication or division operators in the sense that the default associativity for exponentiation goes right to left instead of left to right. So unless we mess it up by placing parenthesis, 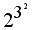 should mean
should mean 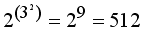 not
not 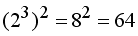 . This leads to the obvious fact that if we take the levels of exponents higher (i.e., 2^3^4^5^3), the numbers can become quite big. But let's not make life miserable. We being the good guys would force the ultimate value to be no more than 10000.
. This leads to the obvious fact that if we take the levels of exponents higher (i.e., 2^3^4^5^3), the numbers can become quite big. But let's not make life miserable. We being the good guys would force the ultimate value to be no more than 10000.