|
在電腦(電子計算機)的溝通中,不像人類是使用十根手指頭十進位來計算,
電腦在硬體上是使用二元運算,也就是所謂的二進位計算法。
所以,在這我們來看一下十進位與二進位的運算。
10進位和 N 進位轉換:
- 10進位轉2進位
(10進位與2進位關係)
範例: 23 轉成 2進位 (一樣連除法/短除法,可轉換N進位)
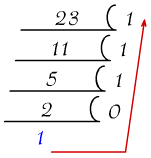
23 = 10111(越後面除出來的餘數,為越高位)
- 2進位轉10進位
請將 10111 轉成10進位
10111 = 1x24 + 0x23 +
1x22 + 1x21 + 1x20
= 1x16 + 0 + 1x4 + 1x2 + 1x1
= 23.
請各位算一下 83 的二進位是多少呢?
| ... |
29 |
28 |
27 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
| ... |
512 |
256 |
128 |
64 |
32 |
16 |
08 |
04 |
02 |
01 |
| |
|
|
|
|
|
? |
|
|
|
|
10進位對應2、8、16進位換算表,如下:
十進位(10)
Decimal |
二進位(2)
Binary |
八進位(8)
Octal |
十六進位(16)
Hexadecimal |
| 0 |
0000 |
00 |
0 |
| 1 |
0001 |
01 |
1 |
| 2 |
0010 |
02 |
2 |
| 3 |
0011 |
03 |
3 |
| 4 |
0100 |
04 |
4 |
| 5 |
0101 |
05 |
5 |
| 6 |
0110 |
06 |
6 |
| 7 |
0111 |
07 |
7 |
| 8 |
1000 |
10 |
8 |
| 9 |
1001 |
11 |
9 |
| 10 |
1010 |
12 |
A |
| 11 |
1011 |
13 |
B |
| 12 |
1100 |
14 |
C |
| 13 |
1101 |
15 |
D |
| 14 |
1110 |
16 |
E |
| 15 |
1111 |
17 |
F |
| 16 |
- |
20 |
10 |
- 10進位轉8進位
同理,10進位轉8進位也是一樣的道理。
連除。
轉換 N 進位,那同學同理可推怎麼去做了嗎?
- 8進位轉10進位
同理,轉換回10進位,只要將相對應的位元乘以8n位數即可得到.
N進位換算回10進位也是一樣.
- 2進位和8進位關係
如果觀察力強的同學,
不難發現,二進位和八進位是什麼關係?
我們將二進位以三個位數切割一組.
1101(2)=001,101
(不足位數則補零,需補兩位數, 藍色部分)
= 1 , 5 (8)
- 電路、數位邏輯電路的應用
想想為什麼不用十進位來製作計算電路?而是使用二進位的方式呢?


- 10進位小數換成2進位小數
將小數點以下位數乘以2,
所得到的個位數為二進位的小數,
依順序往低位排列.
範例:0.375
0.375x2 = 0.750
0.750x2 = 1.500
0.500x2 = 1.000
所以,二進位小數為 .011
倒推驗算一次
.011 = 0x2-1 + 1x2-2 +
1x2-3
= 0x0.5 + 1x0.25 + 1x0.125
= 0.375
|