|
- 遞迴函數
簡單來說,函數以直接或間接的方式,定義(呼叫)自己,稱為遞迴函數。
說明:f(x) = f(x-1) + 1
上述函數,會有什麼問題呢?
x=3, f(3)=f(2)+1
x=2, f(2)=f(1)+1
x=1, f(1)=f(0)+1
...
(無窮...? 如何終止)
- 遞迴 vs 迴圈
之前在迴圈時,介紹的求和公式,如果大家還有印象,
讓我們對照一下迴圈(重複結構),跟遞迴方式的差異:
| i |
sum=sum+i |
迴圈結果 |
遞迴作法 |
備註 |
| 1 |
sum=0+1 |
1 |
S(1)=1 |
|
| 2 |
sum=1+2 |
1+2 |
S(2)=
S(1)+2 |
|
| 3 |
sum=(1+2)+3 |
1+2+3 |
S(3)=
S(2)+3 |
|
| |
... |
... |
... |
|
| k |
sum=sum+k |
1+2+3+...+k |
S(k)
= S(k-1)+k |
|
可以發現以迴圈來執行,是利用其重複執行的特性,將迴圈變數加總起來,
但以遞迴的方式,則是(不斷)呼叫自己,將傳遞的參數逐漸遞減,達到加總。
所以,各位可以將此求和的遞迴函數程式碼完成嗎?
int sum(int n)
{
if(結束條件成立){
return
預設值;
}
return sum(n-1)+n;
}
可以的話,在main()中呼叫此函數看看是否ok...
#include <stdio.h>
int sum(int n)
{
...
}
main()
{
int n;
printf("Input n:");
scanf("%d", &n);
printf("1+2+3+4...+n=%d\n",
sum(n) );
}
[練習]:
請用遞迴函數的方式,寫一個程式,
輸入n,
輸出 1x2 + 2x3 + 3x4 +...+ (n-1)xn 的結果.
- 遞迴函數定義:
自己呼叫自己的函式。需要符合下列事項:
注意:
1. 尋找遞迴的規律,觀察歸納出符合的關係式。
2. 在某些條件狀況下,遞迴要能結束;簡單說就是要有終止條件。
讓我們來看費氏數列,費氏數列的關係,該項數值是由前兩個數項加起來,
而費氏數列的終點,是f(0)=0,f(1)=1,
讓我們練習一下下面的範例。
- 範例:
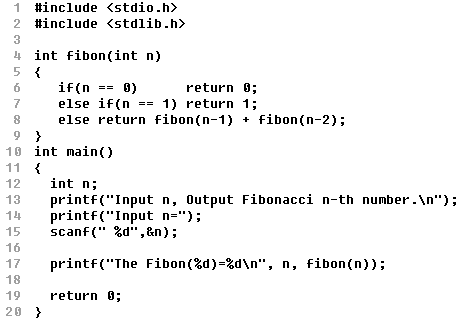
請編譯執行上述程式,測試以下輸入,
n=3,
n=5,
n=30,
n=40,
看看結果為何?
(改善方法)
- 練習:
求ab ?
輸入a, b
輸出 a 的b次方(利用遞迴)
- 常見應用題:
- 求和Summation
- 階層Factorial(n!)
- 最大公因數(GCD, Greatest Common
Divisor)
- 二項係數(Binomial Coefficient):
C(m,n)
- 費氏數列 Fibonacci Number
- 河內塔(Hoari)
|
|